C++ – 树的重心 Link Cut Centroids

题目传送门

性质

1. 删除重心后所得的所有子树，节点数不超过原树的1/2，一棵树最多有两个重心；2.树中所有节点到重心的距离之和最小，如果有两个重心，那么他们距离之和相等；
2. 两个树通过一条边合并，新的重心在原树两个重心的路径上；
3. 树删除或添加一个叶子节点，重心最多只移动一条边；
4. 一棵树最多有两个重心，且相邻。

思路

如果找到只有一个重心，那么直接删一个重心的直连边然后加回去就好了。
如果找到两个重心，那么在其中一个重心上找到一个直连点不是另一个重心，删除连另外一个就好了。

如何求树的重心？
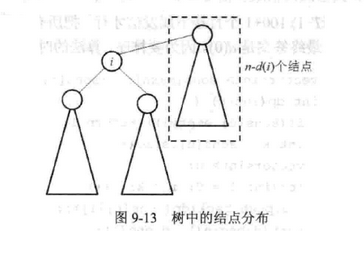
先任选一个结点作为根节点，把无根树变成有根树。然后设 siz[x] 表示以 x 为根节点的子树节点个数。转移为 siz[x] = Σ(i = 0; i <= v[x].size()) siz[v[x][i]] ; 设 son[x] 表示删去节点x后剩下的连通分量中最大子树节点个数。其中一部分在原来 i 其为根的子树。 son[x] = max(son[x], siz[v[x][i]]) ; 另外一部分在x的“上方”子树有 n – siz[x] 个。  son[x] = max(son[x], n – siz[x]) ;

#include<cstdio>
#include<algorithm>
#include<vector>
#include<queue>
#include<utility>
#include<cstring>
#include<iostream>
#define go(a,b,c) for(int a=b;a<=c;a++)
using namespace std;
int t, n, sz[100010], f1, f2, son[100010];
vector<int> v[100010];
void dfs(int x, int fa) {
    sz[x] = 1;
    son[x] = 0;
    int len = v[x].size();
    go(i, 0, len - 1) {
        int to = v[x][i];
        if (to == fa)
            continue;
        dfs(to, x);
        sz[x] += sz[to];
        son[x] = max(son[x], sz[to]);
    }
    son[x] = max(son[x], n - sz[x]);
    if ((son[x] << 1) <= n) {
        f2 = f1;
        f1 = x;
    }//用性质1判断节点x是否为重心
}
int main() {
    cin >> t;
    while (t--) {
        cin >> n;
        memset(sz, 0, sizeof sz);
        memset(son, 0, sizeof son);
        f1 = f2 = 0;
        go(i, 1, n)
            v[i].clear();
        go(i, 1, n - 1) {
            int x, y;
            cin >> x >> y;
            v[x].push_back(y);
            v[y].push_back(x);
        }
        dfs(1, 0);
        if (!f2)
            cout << f1 << ' ' << v[f1][0] << endl << f1 << ' ' << v[f1][0] << endl;
        else {
            int len = v[f2].size();
            go(i,0,len-1)
                if (v[f2][i] != f1) {
                    cout << f2 << ' ' << v[f2][i] << endl << f1 << ' ' << v[f2][i] << endl;
                    break;
                }
        }
    }
    return 0;
}